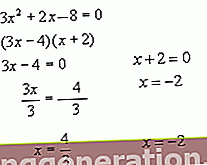definition af ligning
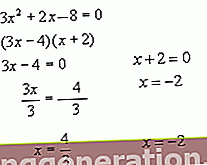I matematik kaldes ligestillingen mellem to algebraiske udtryk en ligning, som kaldes medlemmer af ligningen. I ligninger vises de relaterede gennem matematiske operationer, tal og bogstaver (ukendte).
De fleste matematiske problemer finder deres betingelser udtrykt i form af en eller flere ligninger.
I mellemtiden, når nogen af værdierne af variablerne i ligningen opfylder lighed, vil denne situation blive kaldt ligningen.
Før en ligning kan følgende scenarier forekomme, at ingen af de ukendte værdier når lighed, eller tværtimod, at enhver mulig værdi af det ukendte opfylder det, i dette tilfælde ville vi stå over for det, der kaldes identiteter i matematik, og når to matematiske udtryk falder sammen i uligheden, vil det blive bestemt som ulighed.
Der er forskellige typer ligninger, blandt dem finder vi den funktionelle ligning, som er en, hvor konstanterne og variablerne ikke er reelle tal, men funktioner. Når en differentiel operator vises i nogle af medlemmerne, kaldes de differentialligninger. Så er der polynomligningen, som vil være den, der etablerer ligestillingen mellem to polynomer. På den anden side er første grads ligninger dem, hvor variablen x ikke hæves til nogen magt, hvor 1 er dens eksponent. I mellemtiden er det karakteristiske og differentiale træk ved ligninger kendt som andengradsligninger, at de har to mulige løsninger på det.
Men for astronomi, hvor udtrykket også siger til stede, er en ligning forskellen mellem stedets eller gennemsnitsbevægelsen og den sande eller tilsyneladende, som en stjerne har.
