definition af trigonometriske identiteter
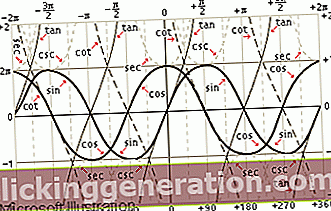Begrebet trigonometriske identiteter er et begreb, der bruges inden for matematik for at henvise til de variable trigonometriske funktioner, der kan findes i en geometrisk figur. Trigonometri er den gren af matematik, der specialiserer sig i analyse og undersøgelse af trekanter, især i former, betydninger og værdier for de forskellige vinkler, der kan eksistere. De trigonometriske identiteter vil så være resultatet af de værdier, der er variable og meget forskellige fra den ene til den anden.
Som med mange elementer i matematik har begreberne eksisteret siden oldtiden, hvor græske filosoffer allerede havde etableret begreberne om funktioner og værdier for vinklerne på geometriske figurer. Disse begreber ville kun blive forbedret i moderniteten i det syttende århundrede, da de blev noteret algebraisk for at kunne udføre alle slags beregninger mellem de forskellige vinkler.
Trigonometriske identiteter kan defineres bredt som alle mulige vinkelvariabler, der kan eksistere i en geometrisk figur. Disse identiteter er altid repræsenteret fra de græske bogstaver som alfa, beta, omega osv. Elementer som grader celsius bruges også til at etablere variablerne for hver identitet. De bedst kendte er dem, der er etableret mellem sinus og cosinus, sinus og tangens osv. Trigonometriske identiteter er forenklede former, der giver os mulighed for at udføre og kende de forskellige funktioner i trigonometri. Alle disse matematikspørgsmål, nærmere bestemt trigonometri, tjener til at organisere de forskellige beregninger, der skal udføres ud fra de specifikke funktioner i hver datatype. Trigonometriske identiteter er meget variable og giver mulighed for at have forskellige muligheder for at repræsentere hver trigonometriske funktion (dvs. værdierne) på varierede og specifikke måder i henhold til hvert enkelt tilfælde.
